Maximum Likelihood Estimation

Estimation Big Picture

Maximum Likelihood Estimation

Let \(X_1, X_2, ..., X_n \stackrel{iid}{\sim} F_{\theta}\)

 

Then the joint distribution of (\(X_1, ..., X_n\)) is given by \(f_{\theta}(x_1,...,x_n)=\prod_{i=1}^{n} f_{\theta}(x_i)\)

 

Now, we define the likelihood function as a function of the fix population parameter \(\theta\) : \(L(\theta)=f_{\theta}(X_1,...,X_n)=\prod_{i=1}^nf_{\theta}(X_i)\)

We want to find the value of \(\theta\) that maximizes the likelihood function and call it \(\hat{\theta}\)

Illustration

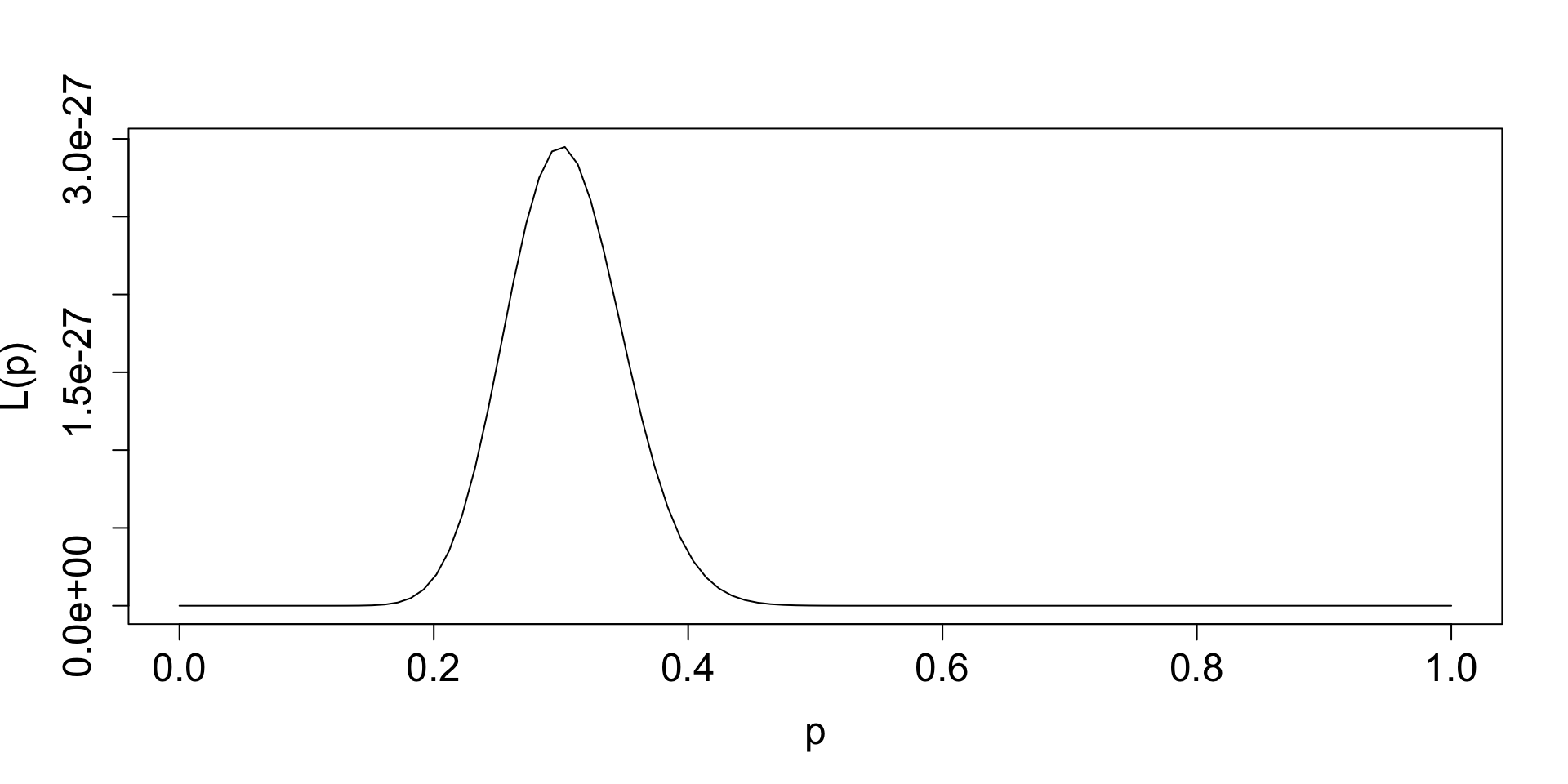
Imagine we have a binary variable (e.g., disease status). n=100, where 30 have the disease.

We can use the Bernoulli distribution, so \(\prod_{i=1}^{n}p^{x_i} (1-p)^{1-x_i}\) and \(L(p)=p^{30}(1-p)^{70}\) , which we can plot over a range of values of \(p\)

General mechanics

1. Assume a distribution for the population
2. Define the likelihood: joint probability of the data
3. Take the log of the likelihood
4. Find the value of \(\theta\) that maximizes the likelihood:
   1. Differentiate the log-likelihood with respect to \(\theta\)
   2. Set the derivative to 0
   3. Solve for \(\theta\)

Evaluating Estimators

• Bias: Average distance from the population parameter

  • Bias(\(\hat{\theta}\)) = \(\mathbf{E}[\hat{\theta}]-\theta\)

• Standard Error (SE): standard deviation of the estimator (i.e., SD of the sampling distribution)

  • STD(\(\hat{\theta}\))= \(\sqrt{\mathbf{E}[\hat{\theta}-\mathbf{E}(\hat{\theta})]^2}\)

• Mean Squared Error (MSE): combines standard error and bias

  • MSE(\(\hat{\theta}\))= \(\mathbf{E}[\hat{\theta}-\theta]^2\) = SE\(^2\) + Bias\(^2\)

Example

Let \(X_1, X_2, ..., X_n \stackrel{iid}{\sim} Poisson(\lambda)\)

Derive the MLE, \(\hat{\lambda}\), and determine if this is an unbiased estimator of \(\lambda\)

\(P(X=x)=\frac{\lambda^x e^{-\lambda}}{x !}\)